結晶内で粒子(イオンや原子など)がどのように配列しているかを表したものを結晶構造と言います。結晶構造は同じような構造の繰り返しとなっており、この繰り返し単位を単位格子といいます。今回は単位格子のうち、体心立方格子と面心立方格子について解説します。
立方体の中心と、頂点の位置に原子が配置している構造を体心立方格子(図a)、頂点に加えて各面の中心にも原子が配置している構造を面心立方格子(図b)といいます。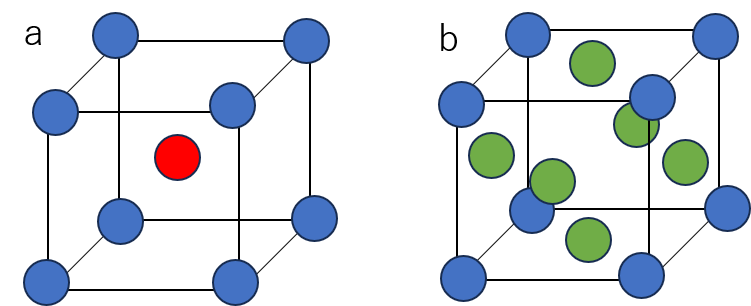
<例題1>
aとbに含まれる原子の数をそれぞれ答えよ。
<解答>
a. 見るからに9個じゃないかと思われるかもしれませんが、実際にはaは何個も繰り返して1つの結晶を形作っています。その一部を切り取ったものです。中央の赤丸は1個の原子ですが、立方体の頂点(青丸)は1/8個分の原子です。ですので、含まれる原子数は
1(赤丸)+ 1/8 (青丸)× 8で、2個となります。
b.こちらも頂点は1/8個で、各面の中心(緑丸)は1/2個分です。立方体を2つ重ねるとちょうど原子1個分になります。含まれる原子数は
1/2 (緑丸)×6 + 1/8 (青丸)×8で、4個となります。
<例題2>
立方体の1辺の長さをxとする。aとbが1種類の原子からできているとき、原子の半径をそれぞれxを用いて表せ。
<解説>
原子半径を求める前に次の図でABの長さとACの長さを立方体の1辺の長さをxとして求めてみてください。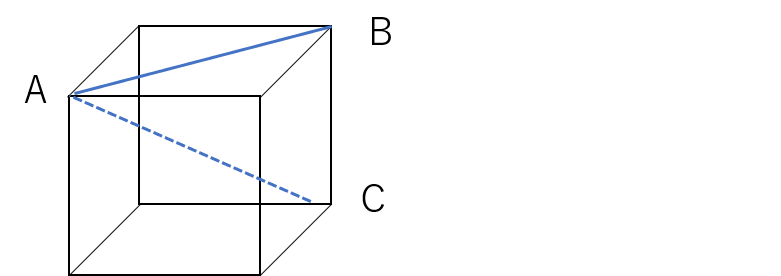
ABは1辺の長さがxの正方形の対角線なので、三平方の定理よりその長さは√2xです。
ACは直角三角形ABCの斜辺なので、三平方の定理より AC2 = AB2 + BC2が成り立ちます。
AB = √2x、BC = xなので、AC2 = 3x2 となり、AC = √3xと求まります。
では、本題の原子半径を求めていきましょう。
まず、体心立方格子ですが、こちらはAC上に図のように原子が並んでいます。つまり半径4個分でちょうどACの長さになります。よって、原子半径は√3x/4となります。
面心立方格子では、AB上に図のように原子が並んでいます。つまり半径4個分でちょうどABの長さになります。よって、原子半径は√2x/4となります。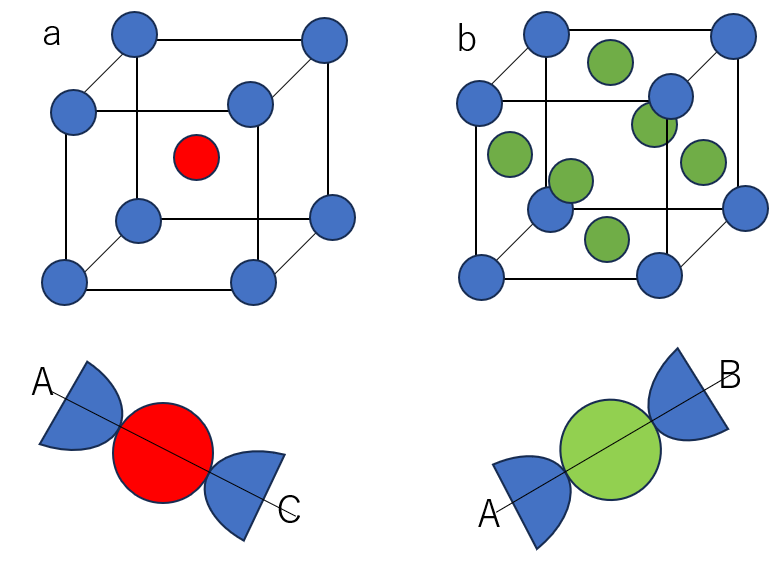

コメント