前回は1文字のたすきがけについて紹介しました。
数学Ⅰ 因数分解 たすきがけ | 猿山高校 (monkey-studying.com)
今回は、2文字のたすきがけを利用した因数分解について解説します。おそらく、高校に入学して最初の中間テストの山場になるのではないかと思います。
これができたら以下の内容にも取り組みましょう。
数Ⅰ 因数分解 2乗-2乗 | 猿山高校 (monkey-studying.com)
まずは、たすきがけの復習をしておきましょう。次の問題を解いてみてください。
<例題1>次の式を因数分解しなさい。
(1) 2x2+5x-3 (2) 3x2-5xy+2y2
<解答・解説>
たすきがけの詳細は別にあるのでそちらをご参照ください。簡単に説明しますと、(1)の場合、かけて2になる数字のペアと、かけて-3になる数字のペアをそれぞれ縦に書いて、斜めに掛け算して足します。その結果が5になるような組み合わせを試行錯誤して見つけるというものでした。図のような組み合わせだと上手くいくので、2x2+5x-3= (x+3)(2x-1)と因数分解できます。(2)もxの他にyが入っていますが、同じ考え方で、3x2-5xy+2y2=(x-y)(3x-2y)と因数分解できます。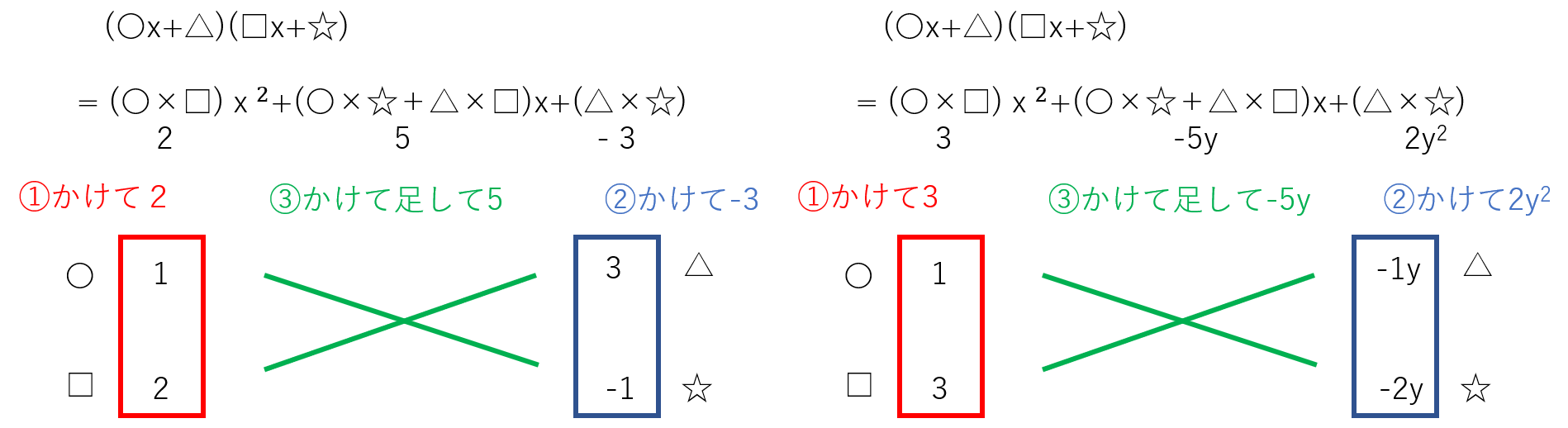
ここまでは、復習でした。今回は次のような因数分解に挑戦しましょう。
<例題2> 次の式を因数分解しなさい。
(1) x2-(3y+4)x+(y+5)(2y-1) (2) 2x2+3xy-2y2-5x-5y+3
<解答・解説>
(1)は一見難しそうですが、今までと同様にできます。かけて1になる数字のペアは1×1だけですし、かけて(y+5)(2y-1)になるペアも(y+5)×(2y-1)だけです。後は、符号に注意してたすきがけをしてみると、図のようにすれば上手くいくので、
x2-(3y+4)x+(y+5)(2y-1) = (x-y-5)(x-2y+1)と因数分解できます。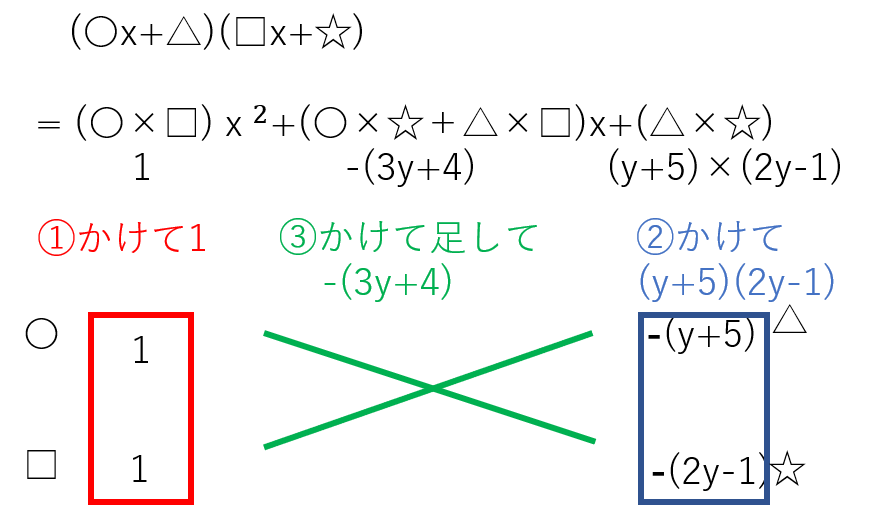
さて、(2)ですね。難しそうですが、(1)みたいな形にすれば解くことができそうです。まず、xについて整理しましょう。つまり、x2がついているもの、xがついているもの、何もついていないものでまとめましょう。
2x2+3xy-2y2-5x-5y+3 = 2x2+(3y-5)x-(2y2+5y-3)
となります。後ろに出てくる 2y2+5y-3 は、例題1(1)のように因数分解できるので、
2x2+(3y-5)x-(2y2+5y-3) = 2x2+(3y-5)x-(y+3)(2y-1)
となります。後はたすきがけで因数分解するだけです。かけて2になるペアは1と2、かけて
(y+3)(2y-1)になるペアは(y+3)と(2y-1)ですね。順番と符号をうまく調整して(3y-5)を作りましょう。3yを作るのを意識すれば-5の方は気にしなくても合うと思います。図のようにすればうまくいきますので、2x2+(3y-5)x-(y+3)(2y-1) = (x+2y-1)(2x-y-3)となります。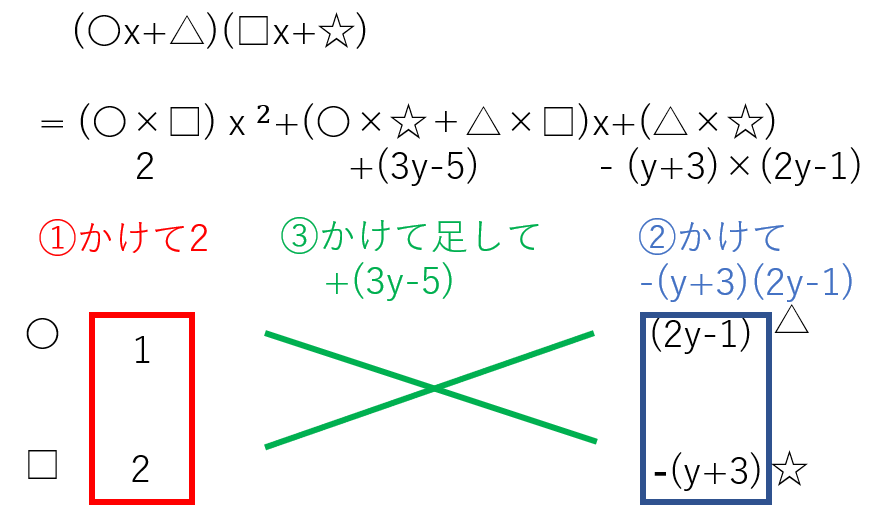
今回のまとめはノートをご参照ください。-scaled.jpg)

コメント