x2+y2のように、xとyを入れ替えても値が変わらない式を対称式と言い、対称式の計算は模試や入試に頻出です。特に、x+yとxyは基本対称式とよばれ、対称式は全て、基本対称式のみを用いて書くことができます。たとえば、x2+y2は、(x+y)2-2xyと書くことができます。では、計算問題を解いていきましょう。
<例題> a+b=1, ab=-1のとき、次の値を求めなさい。
(1) a2+b2 (2) a3+b3 (3) a4+b4 (4) a5+b5
<解答>
(1) a2+b2 = (a+b)2-2abと変形できます。この変形はよく使うので覚えておきましょう。
a2+b2 = (a+b)2-2ab = 12 -2×(-1) = 3
(2) a3+b3 = (a+b)(a2-ab+b2)です。この式は3乗の因数分解の公式なので覚えてしまいましょう。
a3+b3 = (a+b)(a2-ab+b2)= (a+b)(a2+b2-ab)= 1×(3-(-1))=4
(3) a4+b4はどうやれば作れるでしょうか。4乗は2乗を2回すれば作れそうなので、(a2+b2)2でよさそうな気がします。しかし、これは展開すると、a4+2a2b2+b4ですから、2a2b2が余計です。これを引くと、a4+b4 = (a2+b2)-2a2b2 が成り立ちます。
a4+b4 = (a2+b2)-2a2b2=32-2×(-1)2=7
(4) a5+b5も作っていきましょう。(a+b)5を計算しても作れますが、5乗の展開公式を覚えている人はいないでしょう。ここは2乗と3乗を掛け算することで作りましょう。
(a2+b2)(a3+b3) = a5+a2b3+a3b2+b5
ですから、a2b3+a3b2を引けばa5+b5になりそうです。
a5+b5=(a2+b2)(a3+b3)-(a2b3+a3b2)=(a2+b2)(a3+b3)-a2b2(a+b)=3×4-(-1)2×1=11
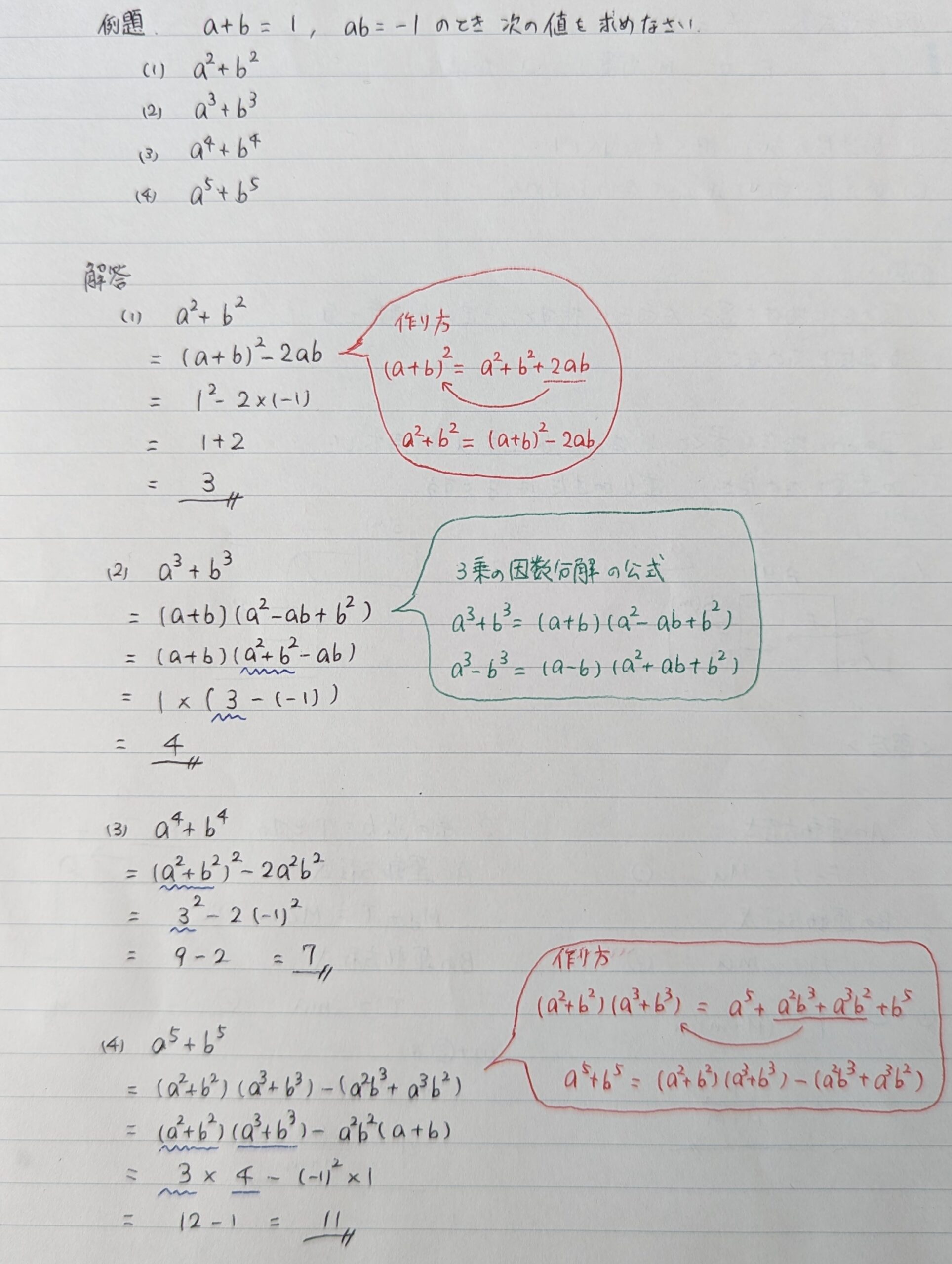


コメント