ここでは2次関数のグラフの書き方について解説します。
まずは中学校で習った内容を復習しておきましょう。
<例題1>次の関数のグラフを書きなさい。また、頂点の座標を答えなさい。
(1) y = x2 (2) y = x2 + 1
<解答>
(1) 適当な数字を入れてつないでみましょう。
x=0のとき、y=1
x=1のとき、y=1
x=-1のとき、y=1
x=2のとき、y=4
x=-2のとき、y=4
ですので、これらの点をつなぐと、図のようになります。
yの値の変化の仕方が変わるところが頂点です。xが0より小さいとyはxが大きくなるほど小さくなりますが、xが0より大きい時はxが大きくなるほどyも大きくなるので境目はx=0の点、つまり点(0,0)が頂点です。
(2) y = x2に1を加えたものですので、(1)のグラフを上に1個ずらしましょう。頂点は点(0,1)です。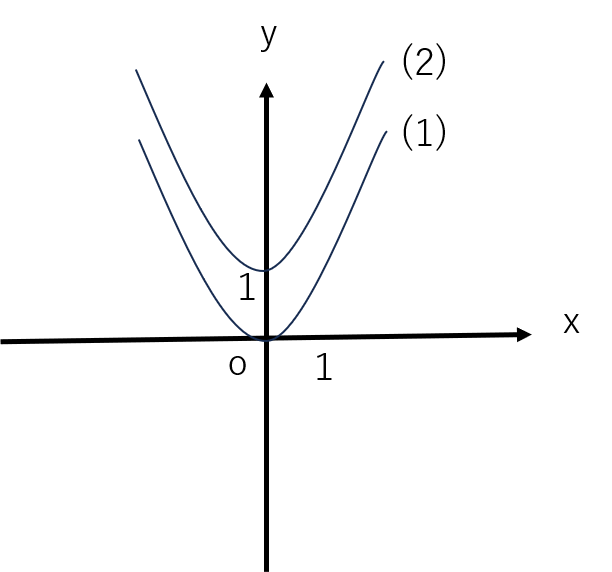
さて、中学では上下の移動しかやらなかったのですが、高校では横方向の移動も学んでいきます。
<例題2>次の関数のグラフを書きなさい。また、頂点の座標を答えなさい。
(1) y = (x-3)2 (2) y = (x+1)2 (3) y = (x-3)2+1 (4) y = -(x+1)2 -1
<解答>
(1) 2乗の中身が0になるxの値が頂点のx座標です。(1)だとx=3ですね。このときy=0ですので、頂点は(3,0)です。あとはこの点が頂点になるように放物線をかけばよいです。
(2) 上と同様に考えると、頂点のx座標はx+1が0になるところなのでx=-1です。このときy=0なので頂点は(-1,0)です。
(3) x-3が0になるのはx=3のときで、このときy=1なので頂点は(3,1)です。
(4) x+1が0になるのはx=-1のときで、このときy=-1なので頂点は(-1,-1)です。他のグラフと違って(4)は最高時の係数が-なので上に凸の放物線となります。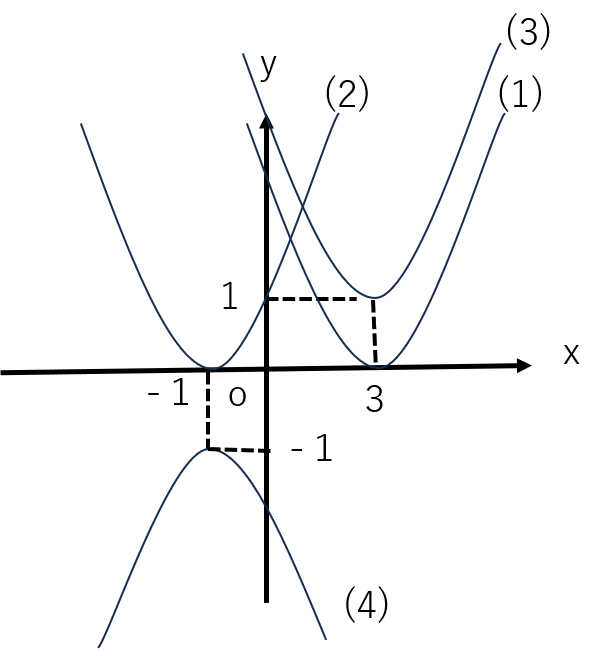

コメント