前回は点電荷が作る電場について解説しました。今回は一様電場と電位の関係について解説します。まずは言葉の解説です。
一様電場とは電場の強さと向きが一様な電場のことで、極板間などに作られます。電場の記号はEをよく使い、単位はN/Cでした。
電位とは、+1 C の電荷を置いたときにその電荷が持つ位置エネルギーのことで、記号はVを使い、エネルギーなので単位はJ/Cです。J/CをV(ボルト)とも書きます。
エネルギーの単位JはN×mで求められることを思い出しましょう。一様電場内で基準点からx [m]だけ離れた点の電位はV = Exで求めることができます(1 Cの電荷が持つ位置エネルギーを想定しています)
図のように、2つの極板で一様な電場を作ったとします。基準からxだけ離れた点の電位V1はV1=Exです。さらにそこからdだけ離れた点の電位V2はE(x+d)と書けます。よって、この2点間の電位差Vは
V=V1 – V2 = E(x+d) – Ex = Edとなり、
E = V/dという式が得られます。電場Eの単位はN/Cでしたが、この式からV/mでもよいということが分かります。
<例題1>
図のように、2つの極板間電位差がVとなるように極板を置いた。A~Dは各極板間の中点であるとする。
(1) A~Dのうち電場の強さが最大なのはどこか。
(2) A~Dのうち電場の強さが最小なのはどこか。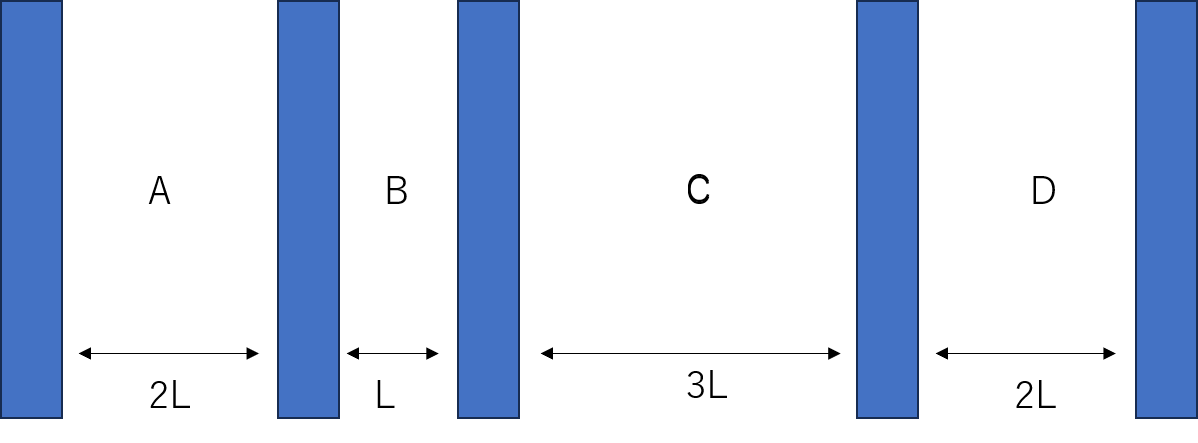
<解説>
E= V/dの式を思い出しましょう。A~Dすべての地点で電位差は同じです。なので分母のd次第でEの大きさが変わります。分子が同じ場合、分母が大きいほど値は小さくなるので、dが大きいほどEは小さく、dが小さいほどEは大きくなります。
(1)最もdが小さいのはB点なので電場の強さが最大なのはB点です。
(2)最もdが大きいのはC点なので電場の強さが最小なのはC点です。
<例題2>
-3 Cの電荷を+10 Vの点から-10 Vの点まで静かに移した。
(1) 外力のした仕事はいくらか。
(2) 静電気力のした仕事はいくらか。
<解答>
(1)
+10 Vの点で電荷の持つ位置エネルギーは (-3 C)×(10 V) = -30 J
-10 Vの点で電荷の持つ位置エネルギーは (-3 C)×(-10 V) = 30 J
ですので電荷の位置エネルギーの変化は 30 J – (-30 J) = 60 J
です。電荷は60 Jの位置エネルギーを獲得したんですね。このエネルギーはどこから来たかというと、外力から仕事をされたからです。よって、外力のした仕事は60 Jです。
(2)
今回の問題では外力と静電気力がつりあっています(そうしないと加速度が生じて電荷が動いてしまう)。この場合静電気力のした仕事は外力のした仕事と大きさが同じで逆向きになります。よって、静電気力のした仕事は-60 Jです。

コメント