物理ではベクトル量と呼ばれる、大きさと向きを併せ持った量を扱います。ベクトルの足し算をどのように行うかをここでは解説します。それほど難しくないですが、物理の計算の基本のきですので、しっかりマスターしておきましょう。
力は「大きさ」と「向き」の2つの要素を持ちます。例えば、「物体に1 Nの力と1 Nの力を加えた」と言っても、実際に物体に作用する力の大きさは分かりません。反対向きに加えていれば0 Nですし、同じ方向に加えていれば2 Nです。
要は単純な足し算ではないということですね。では、力の合成はどのようにするかというと、物体に2つの力を加えた場合、向きは「2つの力を2辺とする平行四辺形の対角線方向」、大きさは「対角線の長さ」になります。図でかくとわかりやすいので、問題に行ってみましょう。
<例題1>図のように物体に2つの力を加えた。2つの力を合成しなさい。

<解答・解説>
(1)は適当に書いてみてください。下の図の赤い矢印が合成した結果です。これは、オレンジで示した2つの力が物体に及ぼす作用は、赤の矢印で示した1つの力が物体に及ぼす作用と同じだということです。
(2)は方向だけでなく、力の大きさも求めてみてください。(1)と同様に書くと、下の図のように長方形が書けて、その対角線が合成した力です。三平方の定理を使うと、2辺の長さが3と4の長方形の対角線の長さは5と求められるので、力の大きさは5 Nとなります。

2力を合成して1つにできるということは、1つの力を2つに分解することもできそうです。平行四辺形の対角線になるならば、好きな方向に分解して構いませんが、(2)のように90°の方向に分解すると問題が解きやすいです。
<例題2>次の図のように物体を置き、大きさFの力で矢印の向きに引っ張った。物体が受ける垂直抗力の大きさを求めよ。物体の質量をm、重力加速度の大きさをgとする。
<解答・解説>
垂直抗力の大きさをNとします。
(1)は簡単ですね。下向きに重力がmg、上向きに力Fと垂直抗力Nがかかるので、
N + F = mg
が成り立ちます。よって、N = mg – F と求まります。
(2)は(1)と違って、Fが斜め上を向いています。なので、鉛直上方向と水平方向に分解しましょう。30°、60°、90°の直角三角形の辺の比は1:2:√3ですので、鉛直上方向の力は1/2Fとなります。よって、N + 1/2F = mg
が成り立つので、N = mg – 1/2F と求められます。
(3)重力を、斜面に平行な向きと垂直な向きに分解しましょう。一般に、直角三角形の3辺の長さは、図のように1、sinθ、cosθと書けるので、斜面に平行な成分の大きさは mgsinθ、斜面に垂直な成分の大きさはmgcosθと書けます。垂直抗力は N = mgcosθ となります。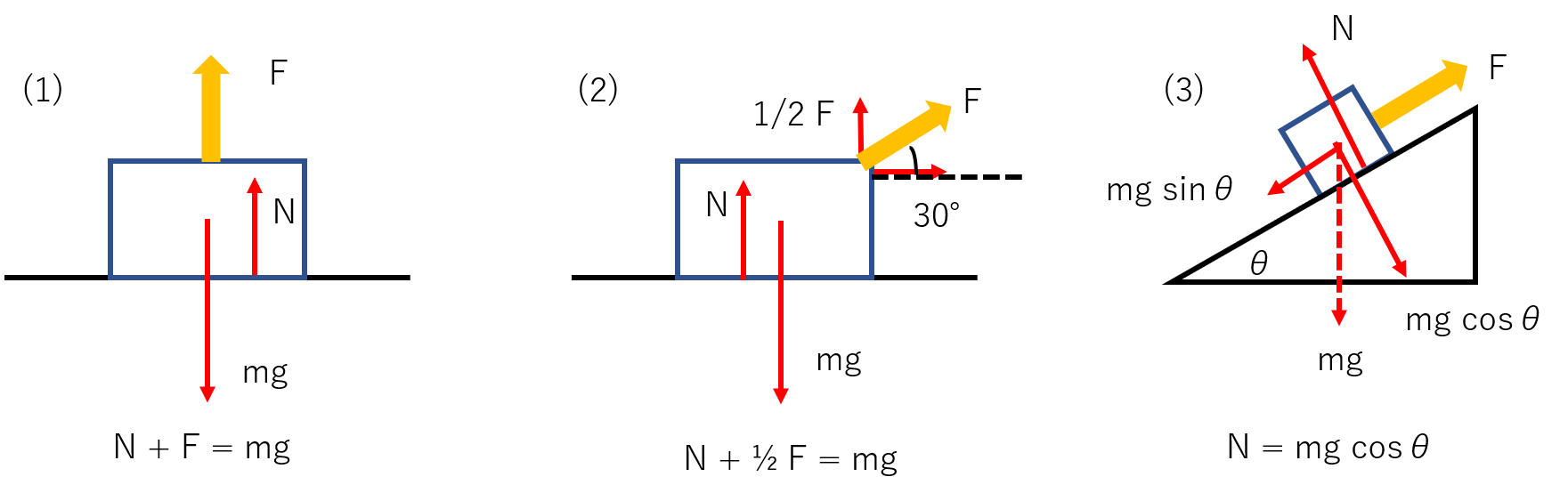

コメント