変圧器とは、交流電流の電圧を変化させるための機械で、図のように鉄心にコイルが巻き付いた構造をしています。電圧を変化させたい交流電流を流す方を1次コイル、もう一方を2次コイルと呼びます。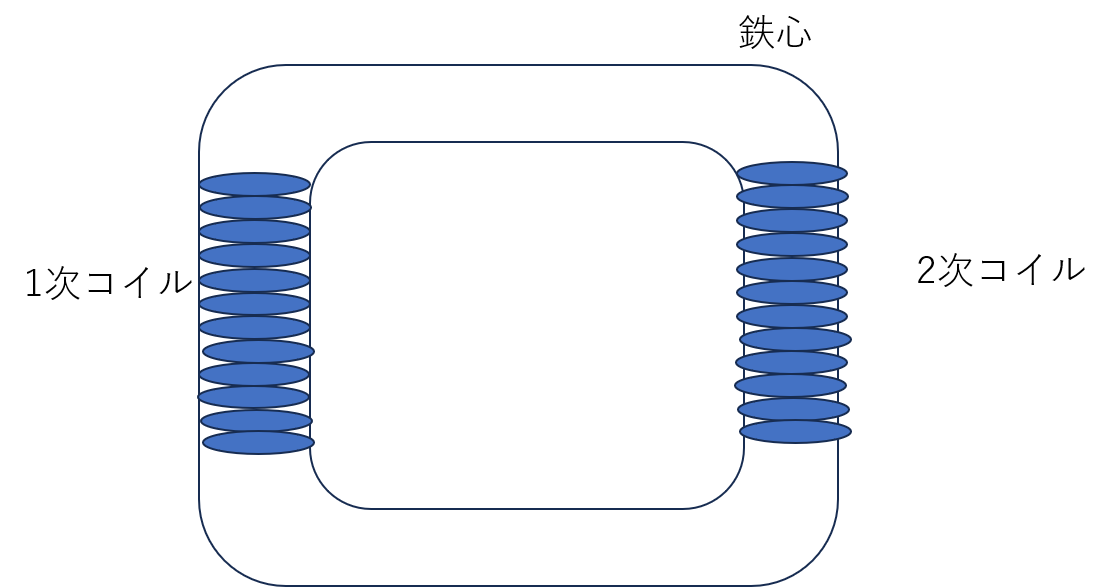
覚えておいてほしいことは以下の2点です。
(1) コイルの電圧は巻き数に比例する
(2) コイルに流れる電流は巻き数に反比例する
<例題>
1次コイル側の電圧は100 V, 2次コイル側の電圧は10 Vであった。
(1) 2次コイルの巻き数は1次コイルの巻き数の何倍か。
(2) 2次コイル側に流れる電流は1次コイル側の何倍か。
<解答>
(1) 巻き数と電圧は比例します。2次コイルの電圧は1次コイルの0.1倍なのでコイルの電圧も0.1倍です。
(2) 巻き数と電流は反比例します。巻き数が0.1倍だったので、2次コイル側を流れる電流は1次コイル側の10倍です。
さて、問題を解くだけならこれだけの話なのですが、もう少し変圧器の仕組み(理論)を深く理解しましょう。「物理」の内容が入るので「物理基礎」しか学習していない方は読み飛ばしていただいても構いません。
<例題2>次の文の空欄を埋めなさい。
1次コイルと2次コイルの巻き数をそれぞれN1,N2
1次コイルと2次コイルの電圧をそれぞれV1,V2
1次コイルと2次コイルの電流をそれぞれI1,I2
1次コイルと2次コイルを貫く磁束はともにΦであるとする。
1次コイルにV1の電圧をかけると、磁束が変化し、( ア )の法則により、大きさ( I )の誘導起電力が発生する。理想的な鉄心であれば2次コイルでも同じだけ磁束が変化するので大きさ( Ⅱ )の誘導起電力が生じる。これらの比をとると、N1/N2 = ( Ⅲ )となり、電圧とコイルの巻き数が比例することがわかる。
また、理想的な鉄心であれば( イ )の法則より、1次コイルと2次コイルの消費電力は等しい。そのためI1/I2 = ( Ⅳ )となり、電流と巻き数は反比例することがわかる。
<解答>
1次コイルにV1の電圧をかけると、磁束が変化し、( 電磁誘導 )の法則により、大きさ( |N1ΔΦ/Δt | )の誘導起電力が発生する。理想的な鉄心であれば2次コイルでも同じだけ磁束が変化するので大きさ( |N2ΔΦ/Δt | )の誘導起電力が生じる。これらの比をとると、V1/V2 = ( N1/N2 )となり、電圧とコイルの巻き数が比例することがわかる。
また、理想的な鉄心であれば( エネルギー保存 )の法則より、1次コイルと2次コイルの消費電力は等しい。そのためI1/I2 = ( N2/N1 )となり、電流と巻き数は反比例することがわかる。
<解説>
ⅠとⅡの解説
教科書的には誘導起電力はV = – N ΔΦ/Δt と-をつけて書かれていますが、今回の問題は「大きさ」を答えるものですので、絶対値をつけております。
Ⅲの解説
V1=|N1ΔΦ/Δt |、V2=|N2ΔΦ/Δt |で比をとると、ΔΦ/Δtが約分されます。
Ⅳの解説
消費電力は電流×電圧で求められます。1次コイルと2次コイルで消費電力が等しいので、
I1V1 = I2V2ですので、
I1/I2 = V2/V1 = N2/N1
となります。

コメント