等加速度直線運動の公式に、x=v0t+1/2at2というのがあります。なかなか覚えにくい公式かもしれませんが、式の意味を考えると覚えやすいと思いますので今回は、この式の意味について解説します。公式が理解出来たら練習問題にも取り組んでみてください。
物理基礎 等速直線運動 練習問題 | 猿山高校 (monkey-studying.com)
<等速直線運動の場合>
等速直線運動する物体の速度(v)と時間(t)の関係を示したグラフは、左図のようになります。初速v0で時間tの間に動いた距離をxとしましょう。距離は速さと時間を掛ければ求まりますから、
x = v0t と書けます。これって図に色を付けた長方形の面積ですよね。つまり、v-tグラフの面積は移動距離(正確には変位)を表します。
<等加速度直線運動の場合>
等加速度直線運動する物体の速度(v)と時間(t)の関係を示したグラフは、右図のようになります。こちらでも、初速v0、加速度aで時間tの間に動いた距離をxとして、xを求める式を考えましょう。時刻tでの物体の速度vは、v = v0 + atと表せます。これにtを掛けるとxになるかというと、そうはなりません。このvは時刻によって変わるからですね。
ではどうすればいいかというと、v-tグラフを使います。v-tグラフの面積がxに相当するのでした。グラフを長方形の部分と三角形の部分に分けて面積を求めると、
x = v0t + 1/2 at2 となります。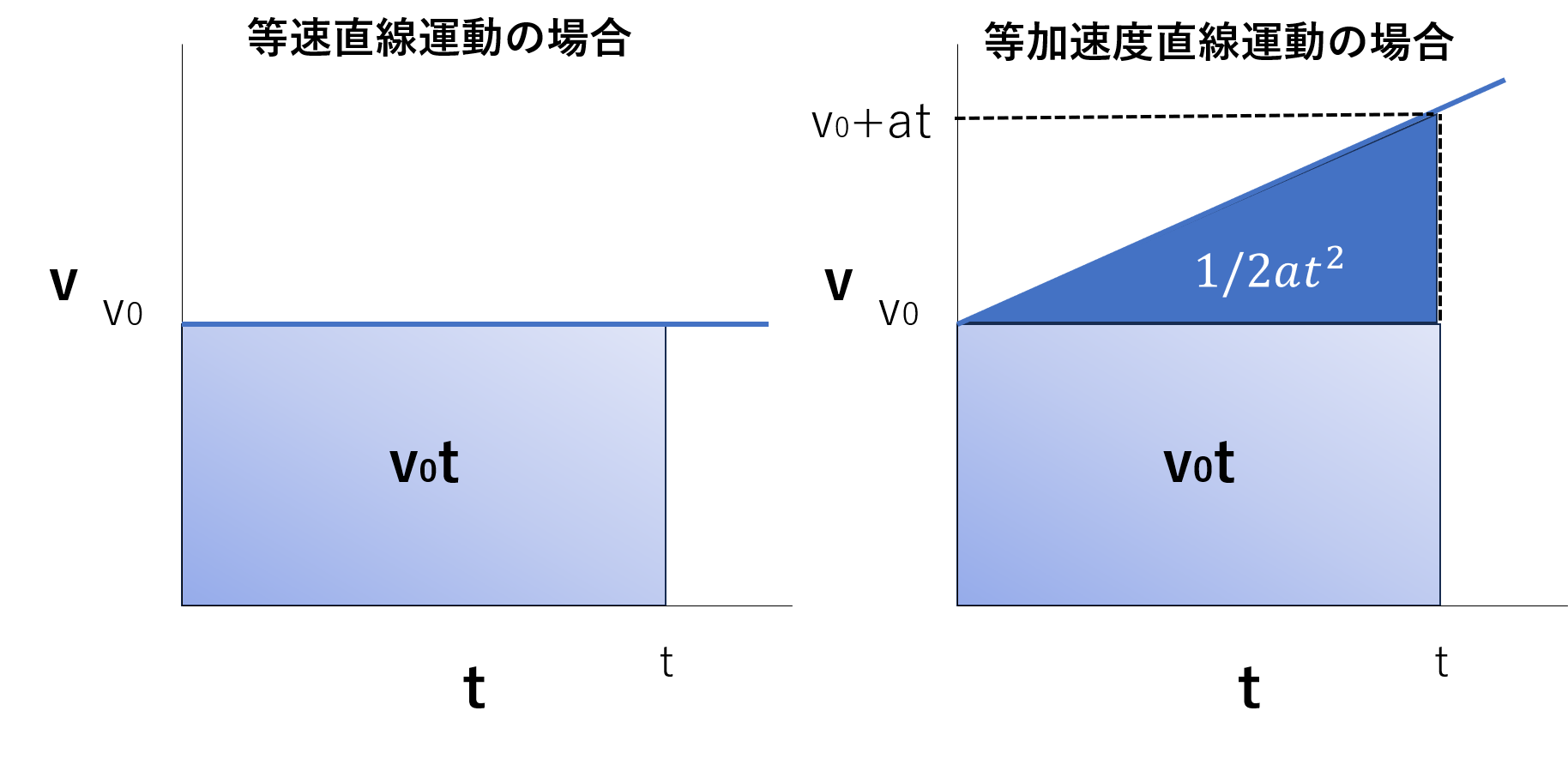
最後に練習問題を解いてみましょう。
<例題>物体が初速6 m/s、加速度-2 m/s2で4秒間等加速度直線した。右向きを正として次の問いの答えなさい。
(1) 物体が最も右に移動したときの時刻と変位を求めなさい。
(2) 4秒後の物体の変位を求めなさい。
<解答>
グラフを書かなくても解けますが、今回はグラフを書いて考えましょう。
4秒後の物体の速度は 6 -2 × 4 = -2 m/sなので、v-tグラフは図のようになります。面積が+の間は右向きに動いた距離、-の間は左向きに動いた距離です。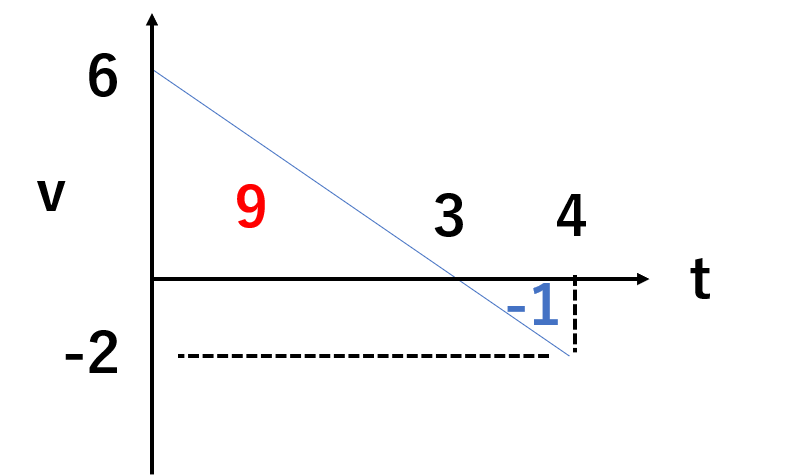
(1) 物体が最も右に移動するのは面積がぎりぎりプラスになるところ(速度が0のところ)なので、3秒後で、変異は9 mです。
(2) 4秒後の時点では、右に9 m、左に1 m移動しているので、変異は8 mです。
今回は以上です。まとめはノートをご覧ください。

コメント