
数学Ⅰで学ぶ因数分解について、3回に分けて解説します。初回の今回はたすき掛けについて解説します。中学校で学んだ因数分解との違いを意識しましょう。
今回の内容が理解できれば以下にも取り組んでみてください。
因数分解②数学Ⅰ 因数分解 たすきがけ(2文字) | 猿山高校 (monkey-studying.com)
因数分解③数Ⅰ 因数分解 2乗-2乗 | 猿山高校 (monkey-studying.com)
まずは、次の例題を解いてみてください。
<例題1>(x+2) (x+3)を展開しなさい。
<解答・解説>
分配法則でやってみると、
(x+2)(x+3) = x2+3x+2x+6 = x2+5x+6
となります。分からない方は中学数学の解説をご覧ください。
では、因数分解に行きましょう。
<例題2> x2+5x+6を因数分解しなさい。
<解答・解説>
因数分解するということは、x2+5x+6を (x+〇)(x+△)の形に戻すということです。 (x+〇)(x+△)を展開してみると、x2+ (〇+△)x+(〇×△)という形になりますから、〇+△が5、〇×△が6になるような数字のペアを見つければ因数分解できます。今回は2と3が上手くいきそうなので、
x2+5x+6 = (x+2)(x+3)となります。ここまでは中3数学の復習でした。
では、高校範囲に行きましょう。高校では次のような因数分解を取り扱います。
<例題3>次の式を因数分解しなさい。
(1) 2x2+5x+3 (2) 6x2+11x+3 (3) 5x2-11x+2
<解答・解説>
中学範囲との違いはx2の項の係数が1ではないことですね。中学範囲では、x2の係数が1だったので、因数分解した形は(x+〇)(x+△)と分かっていました。高校範囲では(〇x+△)(□x+☆)という形になります。これを展開してみると、(〇×□)x2+(〇×☆+△×□)x+(△×☆)となるので、(1)では、〇×□が2で、〇×☆+△×□が5、△×□が3になるような数字のペアを見つければいいことになります。
ですが、このままだと少し考えにくいですよね。そこで、たすき掛けという方法をごご紹介します。次の図を見てください。〇×□が2になるので、例えば1×2というペアが思いつきます。これを縦に書きます。同様に、△×☆が3になるペア、例えば1×3を縦に書きます。これを斜めに掛け算して足します。その結果が5になれば正解です。ならなければ他のペアを探しましょう。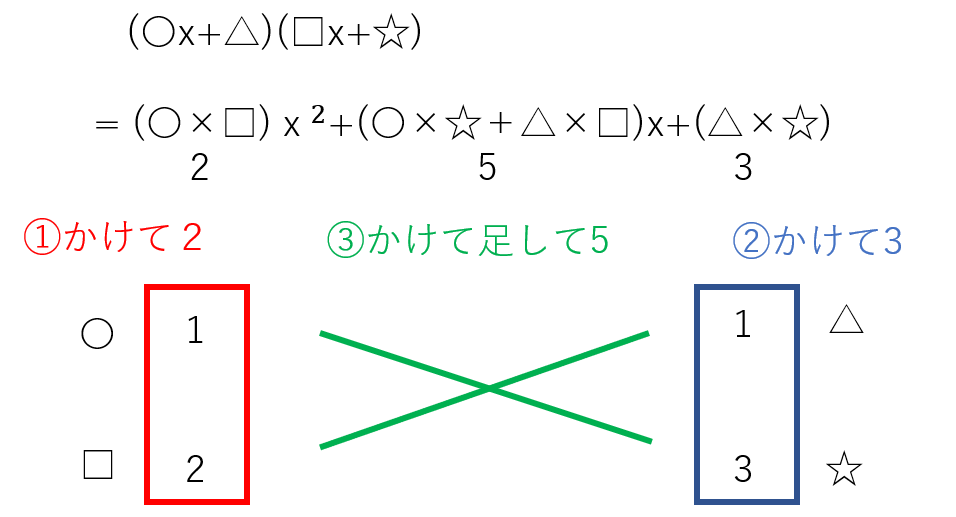
この結果から、2x2+5x+3 = (x+1)(2x+3)と因数分解できます。
(2) (3)も同様にできますのでやってみてください。
答えは以下です。
(2) 6x2+11x+3 = (2x+3)(3x+1)
(3) 5x2-11x+2 = (x-2)(5x-1)

コメント