慣性の法則はご存じでしょうか。物体に外から力が加わらないとき、今の状態を維持しようとする性質のことです。よく電車の例が引き合いに出されます。電車に乗っていると、進行方向とは逆向きに力を受けているように感じますよね。あれが慣性です。実際に何かから力を受けているわけではないですよね。でも、何か力を受けているような気がするということで考えられた見かけの力が慣性力です。慣性力の大きさは、質量(m)×加速度(a)で求めることができ、向きは加速度の逆向きです。
まずは、慣性の法則について問題を解いてみましょう。
<例題1>次の文章を完成させなさい。
前方に加速度運動している電車内では体は電車の(前方・後方)に引っ張られるように感じる。この電車が急ブレーキを踏むと、体は電車の(前方・後方)に倒れる。
<解答・解説>
慣性力は加速度の向きと逆向きに働きますから、前方に加速度運動していれば後方に引っ張られるように感じます。急ブレーキを踏むと加速度は後ろ向きですから、前方に引っ張られる感じがします。
<例題2>
右方向に加速度aで等加速度運動をする電車内に、質量mの物体をつるしたところ、図のように静止した。次の2つの場合で、tanθの値を求めなさい。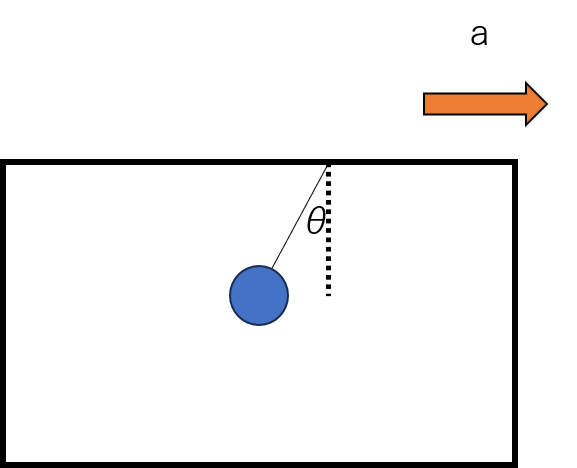
(1) 観測者が電車内にいるとき
(2) 観測者が電車外にいるとき
<解答・解説>
(1) 観測者が電車内にいるときは、加速度と逆向きに大きさmaの慣性力が働くので、力のつり合いの式を立てることができます。物体をつるしている糸の張力をTとすると、
水平方向の力のつり合い: Tsinθ = ma ・・・①
鉛直方向の力のつり合い: Tcosθ = mg・・・②
が成り立ちます。
①より、sinθ = ma/T
②より、cosθ = mg/T
したがって、tanθ = sinθ/cosθ = a/g となります。
(2) 観測者が電車外にいるときは、観測者は慣性力を観測できません。つまり、水平方向に力のつり合いは成り立ちません。では、何の式を立てるかというと、水平方向のTsinθをFとして、F=maの運動方程式を立てます。
運動方程式:Tsinθ = ma・・・①
鉛直方向の力のつり合い: Tconθ = mg・・・②
式の立て方は違いますが、結果的には(1)と同じ式になりますので、tanθ = a/gで結果も同じです(観測者の位置が違うだけで現象としては同じなので当然ですね)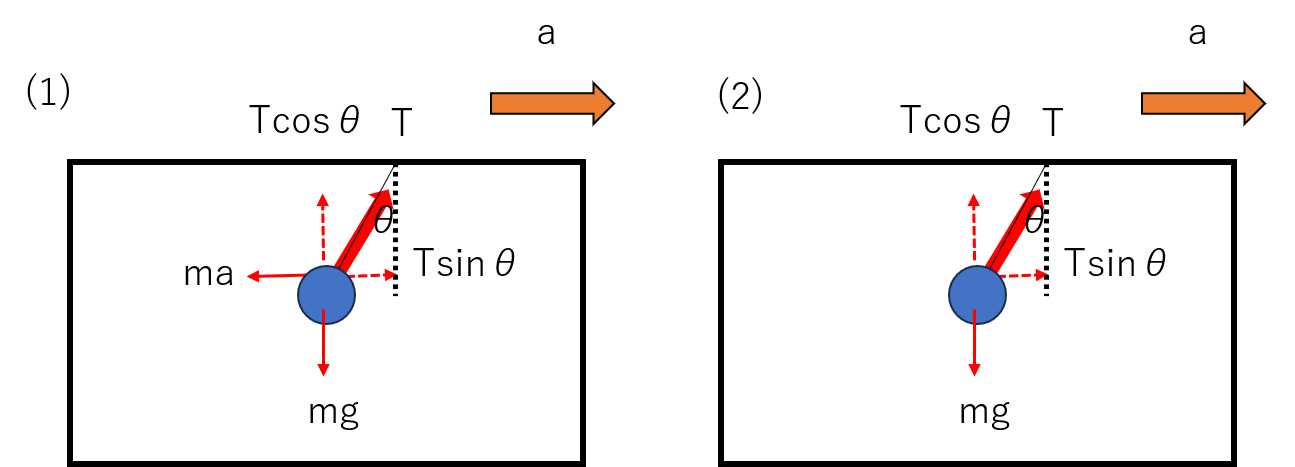

コメント